25 Soal dan Pembahasan Induksi Matematika

Soal 3: Menggunakan Induksi Matematika

Buktikan bahwa untuk setiap bilangan bulat positif n,

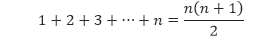
Pembahasan Misalkan P(n) adalah pernyataan 1 + 2 + 3 + … + n = n(n + 1)/2. Kita akan menunjukkan bahwa P(n) bernilai benar untuk semua bilangan bulat positif n.

1. Kita harus menunjukkan bahwa P(1) benar. Dari rumus di atas, pernyataan P(1) menyatakan
   
   dan pernyataan ini dengan jelas bernilai benar.
2. Anggap bahwa P(k) benar. Sehingga hipotesis induksi kita adalah
   
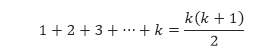
   Kita akan gunakan hipotesis tersebut untuk menunjukkan bahwa P(k + 1) benar, yaitu
   
   Sehingga, kita mulai dengan ruas kiri dan menggunakan hipotesis induksi untuk memperoleh bentuk pada ruas kanan.
   
   Sehingga kebenaran P(k + 1) mengikuti kebenaran P(k), dan kita telah melakukan langkah induksi.

Setelah membuktikan Langkah 1 dan 2, kita dapat menyimpulkan dengan Prinsip Induksi Matematika bahwa P(n) benar untuk semua bilangan bulat positif n.

---

Rangkuman berikut ini memberikan rumus-rumus untuk jumlah pangkat dari n bilangan bulat positif pertama. Rumus-rumus ini sangat penting dalam kalkulus. Rumus 1 telah kita buktikan dalam Contoh 2. Rumus-rumus yang lain juga dapat dibuktikan dengan mengunakan induksi matematika.

Soal 4: Menggunakan Induksi Matematika

Buktikan bahwa

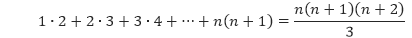
untuk semua bilangan bulat positif n.

Pembahasan Misalkan P(n) adalah pernyataan 1 ∙ 2 + 2 ∙ 3 + 3 ∙ 4 + … + n(n + 1) = [n(n + 1)(n + 2)]/3.

1. Kita akan tunjukkan bahwa P(1) bernilai benar. Berdasarkan rumus di atas, P(1) menyatakan
   
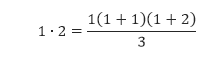
   yang bernilai benar.
2. Anggap bahwa P(k) benar dan kita memperoleh hipotesis induksi sebagai berikut.
   
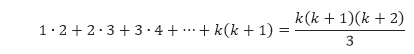
   Hipotesis ini akan kita gunakan untuk membuktikan bahwa P(k + 1) benar. Pernyataan P(k + 1) menyatakan
   
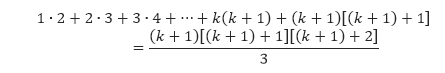
   Kita mulai dari bentuk yang berada di ruas kiri, kemudian kita gunakan hipotesis induksi untuk mendapatkan bentuk pada ruas kanan.
   
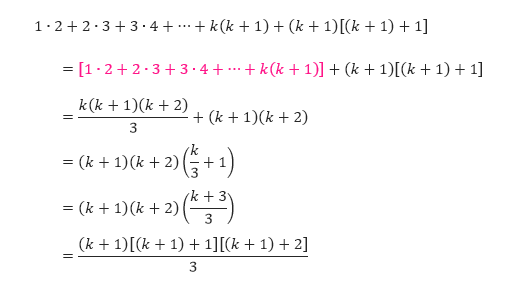
   Sehingga kita telah menunjukkan bahwa P(k + 1) mengikuti P(k). Sehingga kita telah membuktikan langkah induksi.

Berdasarkan Langkah 1 dan 2, kita dapat menyimpulkan dengan menggunakan induksi matematika bahwa P(n) benar untuk semua bilangan bulat positif n.

Soal 5: Menggunakan Induksi Matematika

Buktikan bahwa

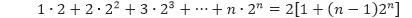
untuk semua bilangan bulat positif n.

Pembahasan Misalkan P(n) adalah pernyataan 1 ∙ 2 + 2 ∙ 2² + 3 ∙ 2³ + … + n ∙ 2ⁿ = 2[1 + (n – 1)2ⁿ]

1. Pertama kita buktikan bahwa P(1) benar. Pernyataan ini menyatakan
   
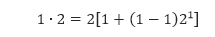
   yang dengan jelas bernilai benar.
2. Selanjutnya, kita anggap bahwa P(k) bernilai benar dan menghasilkan hipotesis induksi sebagai berikut.
   
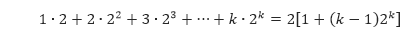
   Hipotesis induksi tersebut akan kita gunakan untuk membuktikan kebenaran P(k + 1). Pernyataan P(k + 1) mengatakan
   
   Kita mulai dari ruas kiri, kemudian kita gunakan hipotesis induksi untuk mendapatkan bentuk yang berada di ruas kanan.
   
   Sehingga pada Langkah 2 ini kita telah membuktikan bahwa jika P(k) benar maka P(k + 1) juga benar.

Jadi, berdasarkan Langkah 1 dan 2, dengan menggunakan induksi matematika kita dapat menyimpulkan bahwa P(n) bernilai benar untuk semua bilangan bulat positif n.

Halaman: 1 2 3 4 5 6 7 8