Penerapan Turunan: Masalah Optimalisasi

Salah satu penerapan kalkulus yang paling umum adalah penentuan nilai maksimum dan minimum. Hal tersebut dapat diamati dengan seberapa sering kita mendengar atau membaca istilah keuntungan terbesar, biaya terkecil, kekuatan terbesar, dan jarak terjauh. Sebelum kita menguraikan strategi untuk menyelesaikan permasalahan seperti itu, perhatikan contoh berikut.

Contoh 1: Menentukan Volume Terbesar

Suatu perusahaan ingin merancang suatu kotak terbuka yang memiliki alas persegi dan luas permukaan 108 cm², seperti yang ditunjukkan gambar di bawah. Berapakah panjang, lebar, dan tinggi kotak tersebut agar menghasilkan kotak dengan volume terbesar?

Pembahasan Karena kotak tersebut memiliki alas persegi, maka volumenya

Persamaan ini disebut sebagai persamaan primer karena persamaan tersebut memberikan rumus untuk nilai yang akan dioptimumkan. Luas permukaan kotak tersebut adalah,

Karena V akan dimaksimumkan, maka kita perlu menulis V hanya ke dalam satu variabel. Untuk itu, kita harus menyelesaikan persamaan 108 = x² + 4xt dalam t yang memuat variabel x. Sehingga dihasilkan t = (108 – x²)/(4x). Dengan mensubstitusi nilai t tersebut ke dalam persamaan primer, didapatkan

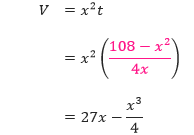
Sebelum menentukan nilai x mana yang dapat menyebabkan V maksimum, kita terlebih dulu harus menentukan domain fungsi V, yaitu nilai x yang masuk akal dalam masalah ini. Kita tahu bahwa V ≥ 0. Kita juga tahu bahwa nilai x yang masuk akal adalah nilai yang tidak negatif dan luas alas (A = x²) memiliki nilai maksimum 108, sehingga domain fungsi tersebut adalah

Untuk memaksimumkan V, kita tentukan nilai kritis fungsi V pada selang (0, √108).

Sehingga diperoleh nilai kritis x = ±6. Kita tidak perlu mempertimbangkan x = –6 karena terletak di luar domain. Kita tentukan nilai V pada nilai kritis dan kedua ujungnya, diperoleh V(0) = 0, V(6) = 108, dan V(√108) = 0. Jadi, V akan bernilai maksimum pada x = 6, dan ukuran kotak yang dimaksud adalah 6 cm × 6 cm × 3 cm.

Pada Contoh 1, kita menyadari bahwa terdapat tak hingga banyak kotak terbuka yang memiliki luas alas 108 cm². Untuk memulai menyelesaikan permasalahan tersebut, kita harus menanyakan kepada diri kita sendiri bentuk kotak yang seperti apa yang dapat menghasilkan volume maksimum. Apakah kotak panjang, pendek, atau kotak yang menyerupai kubus?

Kita bisa mencoba untuk menghitung beberapa volume, seperti yang ditunjukkan gambar di bawah, untuk memprediksi bentuk manakah yang menghasilkan volume maksimum. Ingat bahwa kita tidak siap untuk menyelesaikan masalah sampai kita dapat mengidentifikasi permasalahan tersebut.

Contoh 1 mengilustrasikan langkah-langkah dalam menyelesaikan permasalahan optimalisasi berikut.

---

Panduan Menyelesaikan Permasalahan Optimalisasi

1. Identifikasi semua kuantitas yang diberikan dan semua kuantitas yang akan ditentukan. Jika mungkin, buatlah sketsa.
2. Tulis persamaan primer untuk kuantitas yang akan dimaksimumkan atau diminimumkan.
3. Reduksi persamaan primer menjadi persamaan yang hanya memuat satu variabel bebas. Hal ini melibatkan persamaan kedua yang memuat variabel bebas persamaan primer.
4. Tentukan domain persamaan primer. Sehingga kita harus menentukan semua nilai yang menyebabkan permasalahan yang diberikan masuk akal.
5. Tentukan nilai maksimum atau minimum yang diinginkan dengan menggunakan teknik kalkulus.

---

Halaman: 1 2 3