Banyak hal yang ingin kita ketahui dapat dihitung dengan integral: luas daerah di antara kurva, volume dan luas permukaan bangun ruang, panjang kurva, jumlah kerja yang diperlukan oleh pipa air untuk mengangkat air dari bawah tanah, gaya pada jembatan penahan air, dan koordinat titik massa di mana suatu bangun ruang akan seimbang. Semua hal tersebut akan didefinisikan terlebih dulu sebagai limit dari jumlah Riemann suatu fungsi kontinu pada selang tutup dan kemudian menghitungnya dengan kalkulus.
Luas Daerah Di Antara Kurva: Rumus Dasar sebagai Limit dari Jumlah Riemann
Misalkan akan dicari luas daerah yang terletak di bawah kurva y = f(x), di atas kurva y = g(x), dan di kanan dan di kiri garis x = a dan x = b (Gambar 1 (i)). Daerah tersebut kebetulan memiliki bentuk yang tidak dapat dicari luasnya dengan menggunakan geometri, akan tetapi jika f dan g adalah sebarang fungsi kontinu, kita dapat mencari luasnya dengan menggunakan integral.
Untuk mencari luas daerah dengan menggunakan integral, pertama kita dekati bidang tersebut dengan n persegi panjang vertikal berdasarkan partisi P = {x0, x1, . . . , xn} dari selang [a, b] (Gambar 1 (ii)). Luas persegi panjang ke-k (Gambar 1 (iii)) adalah
ΔAk = panjang x lebar = [f(ck) – g(ck)]Δxk.

Gambar 1
Kita kemudian mendekati luas daerah tersebut dengan menjumlahkan luas dari n persegi panjang.
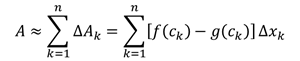
Fungsi f dan g adalah fungsi-fungsi yang kontinu, dengan mengambil limit ||P|| mendekati nol, diperoleh
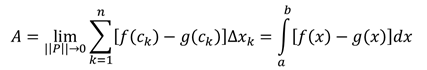
Definisi
Jika f dan g adalah fungsi-fungsi kontinu dengan f(x) ≥ g(x) pada selang [a, b], maka luas daerah di antara kurva y = f(x) dan y = g(x) dari a sampai b adalah integral [f(x) – g(x)] dari a sampai b:
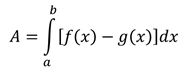
Untuk menggunakan persamaan yang ada di dalam definisi di atas, dilakukan langkah-langkah berikut:
- Gambar kurva-kurvanya dan gambar juga persegi panjangnya. Hal ini untuk menunjukkan yang mana kurva f (kurva atas) dan kurva g (kurva bawah). Hal ini juga dimaksudkan untuk mengetahui batas-batasnya, jika belum diketahui pada soal.
- Cari batas-batas integralnya.
- Tulis persamaan f(x) – g(x). Sederhanakan jika dapat.
- Integralkan [f(x) – g(x)] dari a sampai b. Hasil yang diperoleh merupakan luas daerah yang dimaksud.
Contoh: Cari luas daerah di antara y = cos x dan y = –sin x dari 0 sampai π/2.
Solusi
Langkah 1: Sketsa kurva-kurva tersebut beserta persegi panjang vertikalnya (Gambar 2). Dari gambar diperoleh bahwa kurva atasnya adalah y = cos x, maka f(x) = cos x. Sedangkan kurva bawahnya adalah g(x) = –sin x, sehingga g(x) = –sin x.

Gambar 2
Langkah 2: Batas-batas integralnya sudah diberikan, yaitu a = 0 dan b = π/2.
Langkah 3: f(x) – g(x) = cos x – (–sin x) = cos x + sin x
Langkah 4:
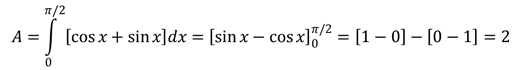
Luas daerah yang diberikan adalah 2 satuan luas. Semoga bermanfaat, yos3prens.

saya punya soal
tentukan persamaan kurva dengan gradien m= dy/dx (x-1) pangkat 3 dan kurva melalui titik A (3,0). mohon bantuannya terima kasih
SukaSuka
m = f'(x) = d/dx (x – 1)³ = d/dx [x³ – 3x² + 3x – 1], Sehingga,
f(x) = integral[x³ – 3x² + 3x – 1] = x⁴/4 – x³ + 3x²/2 – x + c.
Karena kurva tersebut melalui titik A(3, 0), maka
f(3) = 3⁴/4 – 3³ + 3 ∙ 3²/2 – 3 + c = 0
81/4 – 27 + 27/2 – 3 + c = 0
(81 – 108 + 54 – 12)/ 4 + c = 0
15/4 + c = 0
c = -15/4
Jadi, persamaan kurva tersebut adalah f(x) = x⁴/4 – x³ + 3x²/2 – x – 15/4
SukaSuka
kaaa,kalau soalnya carilah luas daerah yang di batasi oleh kurva y=x^-6x+6,garis y=0,dan garis y=6 mohon bantuannya yaa
SukaSuka
Mungkin kurva yang dimaksud adalah y = x² – 6x + 6.
Agar lebih mudah, kita ubah persamaan y = x² – 6x + 6 menjadi,
y = (x² – 6x + 9) – 3
y = (x – 3)² – 3
y + 3 = (x – 3)²
±√(y + 3) = x – 3
3 ± √(y + 3) = x
Sehingga, persamaan y = x² – 6x + 6 setara dengan x = 3 ± √(y + 3). Selanjutnya kita integralkan dengan batas y = 0 dan y = 6.
Luas = int[0, 6] ((3 + √(y + 3)) – (3 – √(y + 3))) dy
= int [0, 6] (2√(y + 3)) dy
= (4/3 ∙ √(y + 3)³) [0, 6]
=(4/3 ∙ √(6 + 3)³) – (4/3 ∙ √(0 + 3)³)
= 36 – (4/3 ∙ √27)
= 36 – (4/3 ∙ 3√3)
= 36 – 4√3
= 4(9 – √3) ≈ 29,0718
Jadi, luas daerah tersebut adalah 29,0718 satuan luas.
SukaSuka
kalau soalnya kaya gini
daerah D dibatasi oleh parabola y = x dan garis y = 2x . gambarlah daerah D dan hitung luasnya
SukaSuka
Pembahasan http://goo.gl/MQ4mXv
SukaSuka
kk mintol tentukan luas daerah yang di batasi oleh kurva y=sin2x dan y=cos x pada kuadran 1!
SukaSuka
Kuadran 1 berada ketika 0° ≤ x ≤ 180°. Selanjutnya kita tentukan titik potong kedua grafik pada selang tersebut.
sin 2x = cos x
2sin x cos x = cos x
2cos x = 1
cos x = 1/2
x = 60°
Sehingga,
L = int[0° – 60°](cos x – sin 2x) dx + int[60° – 180°](sin 2x – cos x) dx
= (sin x + (cos 2x)/2)[0° – 60°] + (-(cos 2x)/2 – sin x)[60° – 180°]
= ([sin 60° – (cos 2 ∙ 60°)/2] – [sin 0° – (cos 2 ∙ 0°)/2] + ([-(cos 2 ∙ 180°)/2 – sin 180°] – [-(cos 2 ∙ 60°)/2 – sin 60°]0
= ([1/2 √3 + 1/4 √3] – [1 – 1/2]) + ([-1/2 – 0] – [1/4 √3 – 1/2 √3])
= (3/4 √3 – 1/2) + (1/2 √3 – 1/2)
= 5/4 √3 – 1
Jadi, luas daerah di antara kurva y = sin 2x dan y = cos x di kuadran 1 adalah 2 √3 – 1 satuan luas.
SukaSuka
minta bantuan kalau soalnya Gradien =x,y
adalah (3×2-8x-5,jika urva itu melalui (2,-10) dan (3,q)
nilai q adalah
SukaSuka
Itu bener persamaan gradiennya, m(x) = 3×2-8x-5 ? Jika iya, berikut penyelesaiannya.
y = int(3×2-8x-5) = int(1 – 8x) = x – 4x^2 + c
Karena grafik dari fungsi tersebut melalui titik (2,-10), maka
-10 = 2 – 4(2)^2 + c
-10 = -14 + c
c = 14 – 10 = 4
Sehingga diperoleh fungsinya adalah y = x – 4x^2 + 4, sehingga
q = f(3) = 3 – 4(3)^2 + 4 = 3 – 36 + 4 = -29.
Jadi, nilai q adalah -29.
SukaSuka
bisa minta tolong bantuannya ^^
jika ada soal f(x)= 2sinx
dan g(x) = cos x
maka berapa luas daerah di antaranya? 🙂
oh yaa.. range’nya antara x 0- 2pi 🙂
SukaSuka
terima kasih 🙂
SukaSuka
Pertama, kita tentukan titik potong grafik f dan g dengan cara substitusi.
2sinx = cosx
sinx / cos x = 1/2
tanx = 1/2
x = 26,57° + k180°
Karena 0° < x < 360°, maka diperoleh batas-batasnya adalah 26,57° dan 206,57° (diperoleh dari k = 0 dan k = 1).
Sehingga luasnya,
L = Int(0°, 26,57°) cosx – 2sinx dx + Int(26,57°, 206,57°) 2sinx – cos dx + Int(206,57°, 360°) cosx – 2sinx dx
L = [sinx + 2cosx](0°, 26,57°) + [-2cosx – sinx](26,57°, 206,57°) + [sinx + 2cosx](206,57°, 360°)
L = 0,236 + 4,472 + 4,236 = 8,944 satuan luas.
Catatan:
Int(a, b) = Integral dari a sampai b
[sinx + 2cosx](a, b) = Nilai sinx + 2cosx dari a sampai b
SukaSuka
tolong saya menyelesaiakn soal seperti ini
1. sketsa dan tentukan luas daerah yang dibatasi oleh kedua kurva
a. f(x)=x(x^2 – 3x + 3), g(x)=x^2
b. g(x)=4/2-x x^2, y=4, x=0
2. tentukan volome benda putar dari persamaan berikut
a. y=x^2, y=4x – x^2, jika diputar mengelilingi
i) sumbu-x ii) garis y=6
b. y= 6-2x-x^2, y=x+6, jika diputar mengelilingi
i) sumbu-x ii) garis y=3
SukaSuka
Untuk soal nomor 1, tolong diperjelas, g(x)=4/2-x x^2 ?
Pembahasan soal nomor 2 dapat dilihat di http://goo.gl/Xni5X.
SukaSuka
tolong bantu saya dengan soal” seperti ini.
1. Hitung isi benda. Bila lingkaran x2 + y2 = a2 diputar mengelilingi sb x.
2. Hitung panjang busur dr grafik y=Ln CSEC X. Untk x dari x=0 sampai x=phi/6.
Terima kasih mohon bantuannya.
SukaSuka
Soalnya persis dengan komentar sebelum ini. Pembahasannya silahkan lihat pada link di komentar sebelum ini. Thx
SukaSuka
tolong bantu saya dengan soal” seperti ini.
1. Hitung isi benda. Bila lingkaran x2 + y2 = a2 diputar mengelilingi sb x.
2. Hitung panjang busur dr grafik y=Ln CSEC X. Untk x dari x=0 sampai x=phi/6.
Terima kasih mohon bantuannya.
SukaSuka
Pembahasan: http://goo.gl/T8ZMZ
SukaSuka
mav sya mau bertanya jika ad prtnyaan luas daerah diantara grafik y=2-x2 dan y3=x2. .
Mhon dibantu. .
Terima kasih.
SukaSuka
Pembahasan: http://goo.gl/T8ZMZ
SukaSuka