Melukis suatu persamaan pada koordinat Cartesius sama dengan memplot semua titik yang memenuhi persamaan tersebut. Misalkan kita akan melukis persamaan y = x + 1 pada koordinat Cartesius. Titik apa saja yang dilalui oleh persamaan tersebut? Tentunya banyak sekali. Berikut ini hasil plot dari beberapa titik yang memenuhi persamaan y = x + 1.

Dari kiri ke kanan, titik-titik yang kita plot semakin banyak. Apa yang dapat kalian peroleh dari gambar di atas? Bagaimana kalau titik-titik yang kita plot ditambah lagi? Bagaimana kalau semua titik yang memenuhi y = x + 1 diplot? Ya, apabila semua titik-titik yang memenuhi persamaan y = x + 1 kita plot, akan membentuk garis lurus.
Grafik dari fungsi linear, y = ax + b atau px + qy + r = 0 berbentuk garis lurus.
Karena grafik dari fungsi linear berbentuk garis lurus, selanjutnya fungsi linear kita sebut sebagai persamaan garis lurus. Contoh-contoh dari persamaan garis lurus lainnya adalah y = x – 6, y = 3x – 7, 2x + 4y – 1 = 0, dan 3x – 8y + 8 = 0. Karena kita telah mengetahui bentuk dari grafiknya, kita tidak perlu untuk memplot banyak titik untuk menggambar grafiknya. Kita hanya perlu memplot 2 titik saja. Mengapa demikian? Karena dengan 2 titik berbeda, kita dapat melukis garis lurus yang melalui titik-titik tersebut.
Misalkan kita akan melukis grafik dari 2x + 3y + 9 = 0. Kita tentukan 2 titik yang memenuhi persamaan tersebut. Apabila kita pilih x = 0, kita mendapatkan y = –3. Bagaimana jika kita memilih x = –3? Ya, kita mendapat y = –1. Sehingga persamaan garis tersebut melalui titik-titik (0, –3) dan (–3, –1). Berikut ini grafik dari persamaan 2x + 3y + 9 = 0.
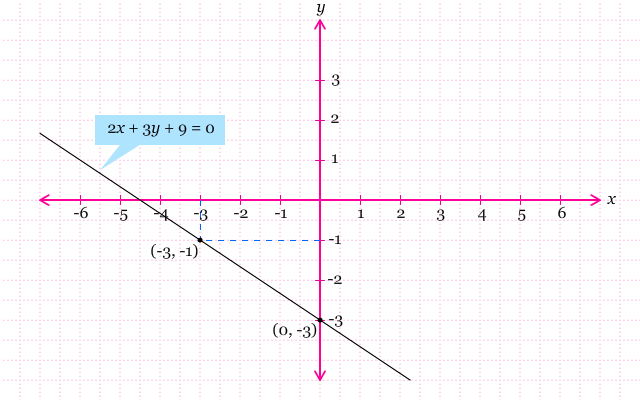
Grafik pada gambar di atas memotong sumbu-x dan sumbu-y. Di titik manakah tepatnya grafik tersebut memotong kedua sumbu tersebut? Suatu grafik memotong sumbu-x ketika y = 0 dan memotong sumbu-y ketika x = 0. Setelah y = o kita substitusi ke persamaan 2x + 3y + 9 = 0, kita mendpatakan x = –4,5. Sehingga grafik di atas memotong sumbu-x di titik (–4,0) dan memotong sumbu-y di titik (0, –3), seperti yang diperlihatkan oleh gambar di atas.
Berikut ini grafik dari persamaan-persamaan x = –3, y = –3, y = 2x – 3, dan x – 2y + 3 = 0.

Yang perlu diketahui, untuk c adalah sembarang konstanta, grafik persamaan x = c merupakan garis lurus yang sejajar dengan sumbu-y (garis vertikal) dan memotong sumbu x di titik (c, 0). Sedangkan grafik persamaan y = c merupakan garis lurus yang sejajar dengan sumbu-x (garis horizontal) dan memotong sumbu-y di titik (0, c). Semoga bermanfaat, yos3prens.

ga paham
SukaSuka
TERIMA KASIH MATERINYA
SukaSuka
… Ga paham…
SukaSuka
mau nanya utk software membuat garis lurus memakai apa ya
SukaSuka